4 Rules to the Meyer Square

I don’t like remembering arbitrary sequences. And on the surface the 16-cut pattern that forms the Meyer’s Square is the exact type of arbitrary sequence that I hate. But is it really? Of course not, because I wouldn’t be writing this article otherwise. 

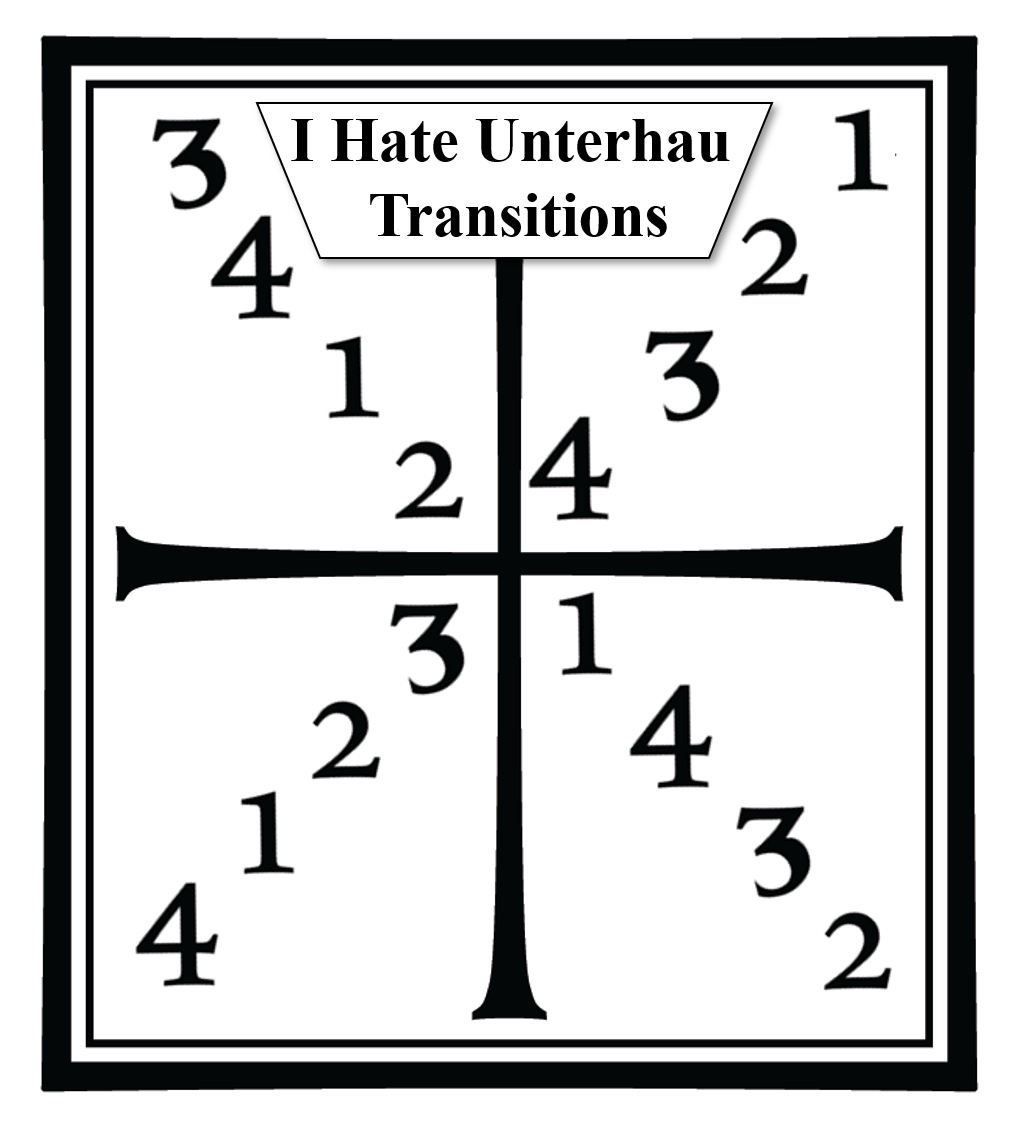
But before we dive in, what exactly is the Meyer’s Square? It is a visual aid to present a cutting pattern described by Joachim Meyer in his 1570 Art of Combat. If you know how to read it you get a pattern of 16 cuts. Go ahead and try:

There are probably a dozen different ways to interpret this based on the picture alone, but I’ll let ol’ Joachim give a crack at explaining it:

“Now so that you may become better trained at this, you shall always change off with the first cut. Thus once you have delivered your first cut to the upper left opening and the second to his lower right opening and so forth as I have just taught (indicated by the outermost numbers in the adjacent diagram), the you shall cut first at his lower left, the second at his upper right, and so forth, as indicated by the second number in the same diagram. Afterwards cut the first to his lower right, the second to his upper left, and so forth as indicated by the third number. Lastly cut your first at his right, and so forth as indicated by the innermost number.”

If you are still confused in what order to do the cuts, I’ve plotted them out in order:

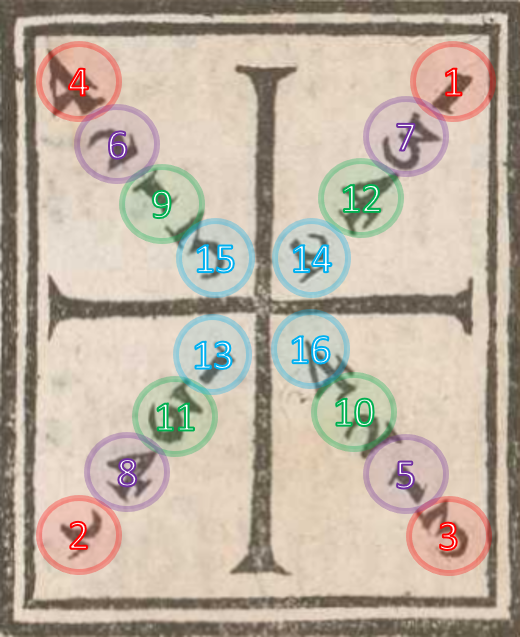
But I already said that memorization is stupid, so what patterns can we pick out to lessen the number of things we have to remember? I’m going to assume that we are cutting all the way through, not stopping in Longpoint. The way you remember it is slightly different if you stop in Longpoint, but you can figure it out in the same way.

(Pedant Warning: I’m going to make up and assign names for parts of the cutting pattern. They are not in Meyer. They may not match something you think you justified from the text. Deal with it.)

(Pedant Warning 2: The name “Meyer’s Square” is something we use for modern convenience. Meyer doesn’t give the diagram or drill a name.)

The Frame

The first and obvious pattern is that each ‘square’ contains all 4 cuts. 

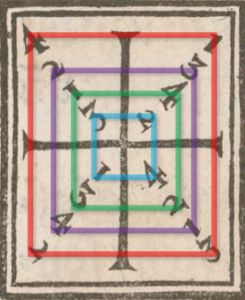
I’m going to call each of these a ‘frame’ because double use of the term square is confusing. So we know that:

Do we have all possible combinations of cuts? We could try to count it out, or we could harness the awesome power of math to figure it out for us. The number of ways to order an arbitrary number of objects (n) is given by the formula: n!

That exclamation point isn’t just there to make the formula look more exciting, it is a mathematical operator called the factorial. (Though factorials quickly produce excitingly huge numbers.)

• 1! = 1
• 2! = 2 x 1 = 2
• 3! = 3 x 2 x 1 = 6
• 4! = 4 x 3 x 2 x 1 = 24

So this indicates that Meyer is holding out on us. Forget 4, there are 24 possible frames!

The Pair

Further inspection of the Square will show that every cut happens as part of a matching set – I have been creative and named this group of two cuts a Pair. In the figure below you can see some examples, but it would be a huge mess if I did all of them. For the remaining four Pairs you have the option of: a) believing me, or b) checking yourself.

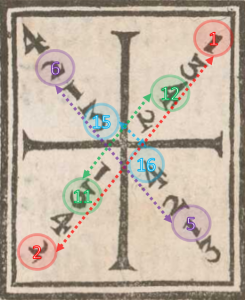
This means that if you did a descending cut from the right at the start of your pair, you do an ascending cut from the left for the second cut of the pair.

Linking Pairs

By our definition each Frame has 2 Pairs*. We know that each pair is on the same line, but we don’t know how to connect the two Pairs within a Frame.

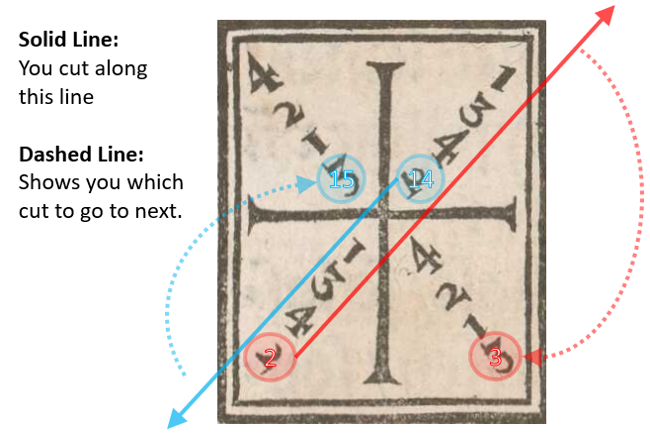
Note that this means you start from the same side you finished the last cut on. Cut 2 and cut 3 are on opposite sides. But at the conclusion of cut 2 your sword is on your right, which is the side you start cut 3 from. 

*At this point a formal logician will get upset because I’ve neglected to define a bunch of other required constraints. Go home. You aren’t fun at parties.

Building a Frame

With the rules I’ve laid out we can make our Frame from any given starting condition. However we don’t know where to start the frame. Given they are all unique, you can just pick the 4 cuts at random, do a Frame of each, and be sure to hit them all. But that wouldn’t be doing THE Meyer Square. And naturally all Meyer practitioners must do the exact sequence as described, lest it lose its mystical power.

i(n) = (f(n) = (-1)n * f(n-1 {f(0) = 1}, (-1)n )

Then it all falls into place with one simple rule. 😀  

Build a Square

And now you have it. Four(ish) simple rules to be able to do the Meyer Square algorithmically. 

Using this approach it isn’t all that difficult to have the Meyer square ‘memorized’ and reproduced in under 5 minutes – though I think memorizing it the hard way is a badge of honor to some people. Or, alternatively we can always try to not miss the forest for the trees, and realize that Meyer put this together more or less based on one higher level rule:

More Math

Above I said that there are actually 24 potential Frames, and Meyer gave us less than half of that. So what would the alternative frames look like?

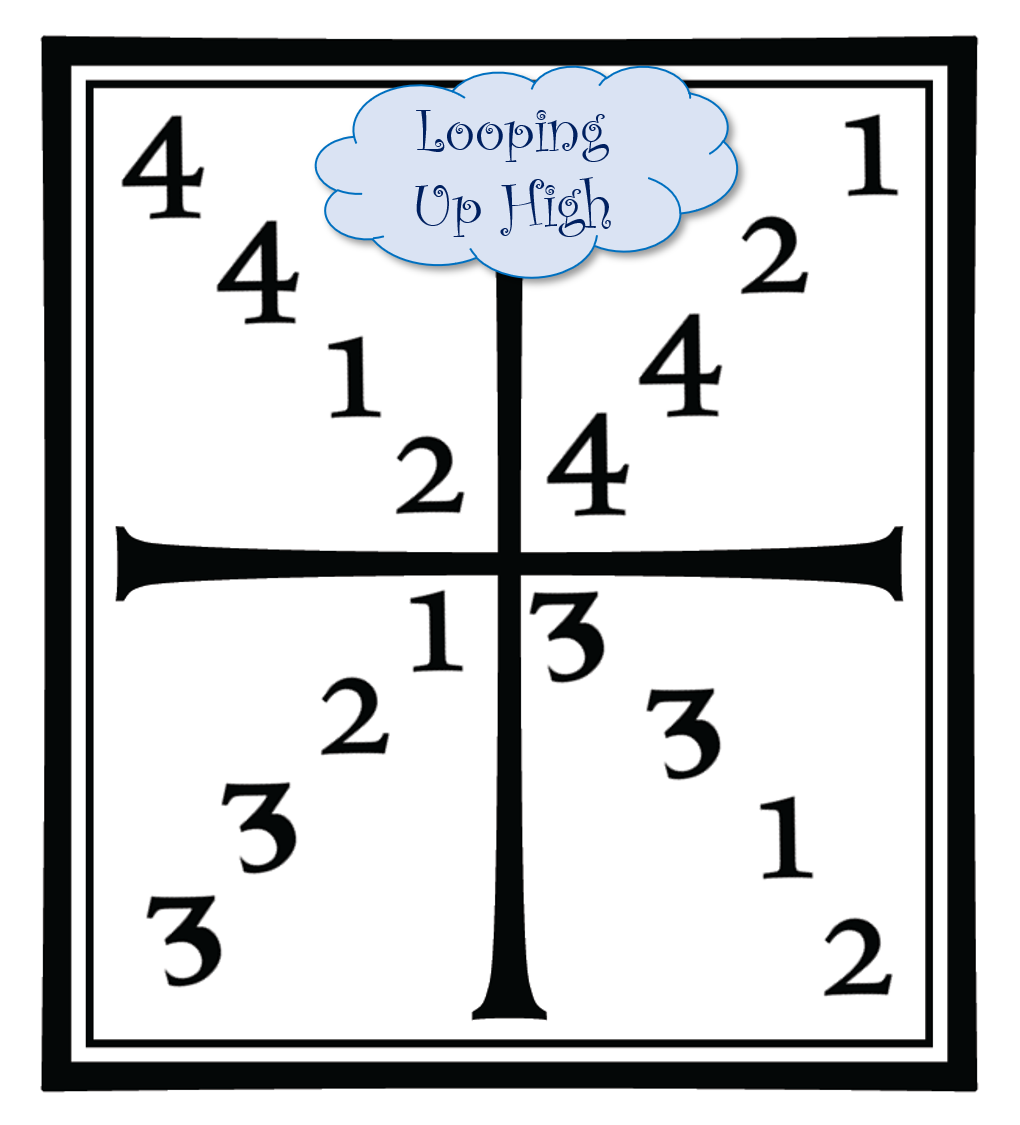
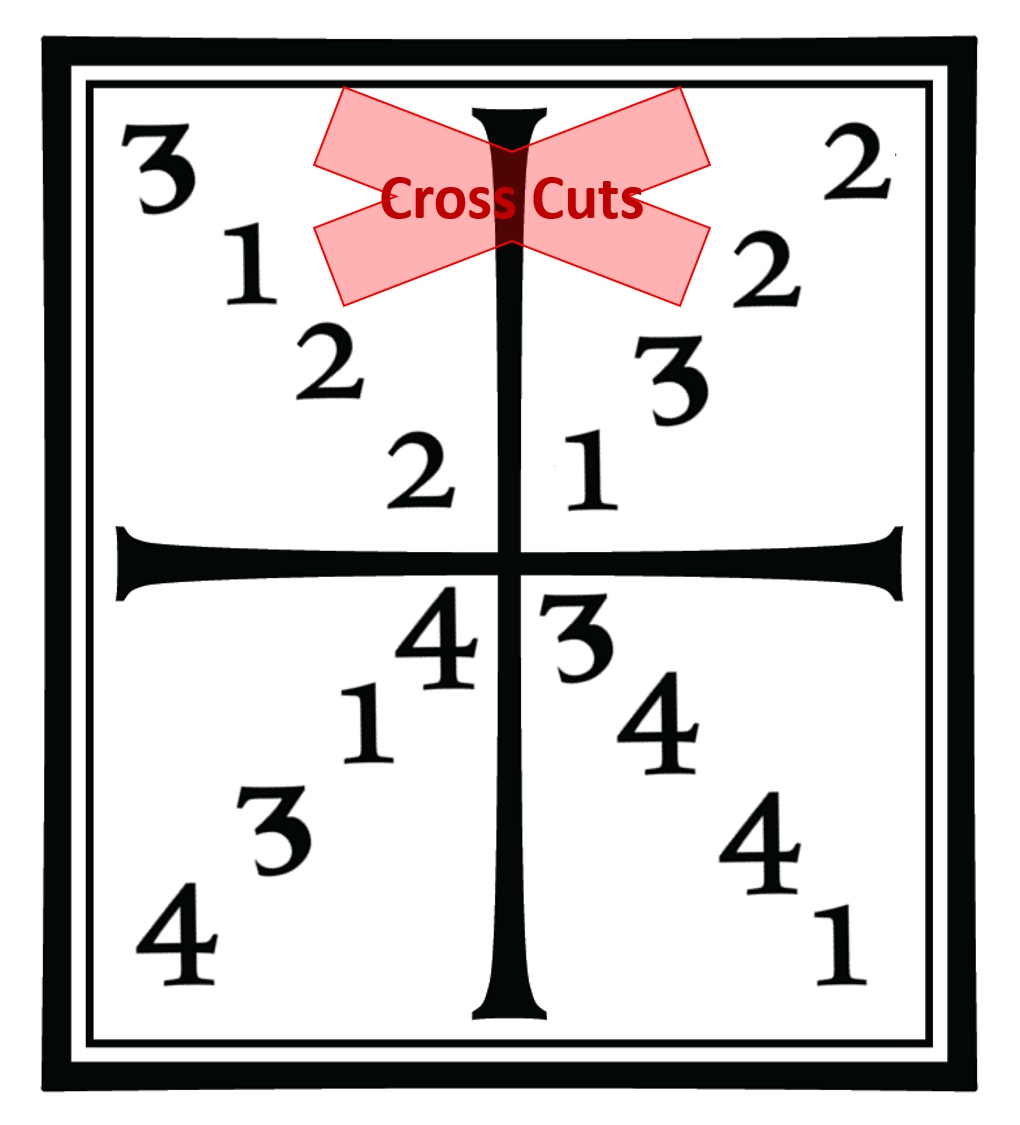
What can we do with this knowledge? How about I try to come up with 5 new Meyer-ish squares with consistent themes, using up all the other Frame combinations. For the first I tried to break as many rules of the Meyer square as possible in the Frame construction:

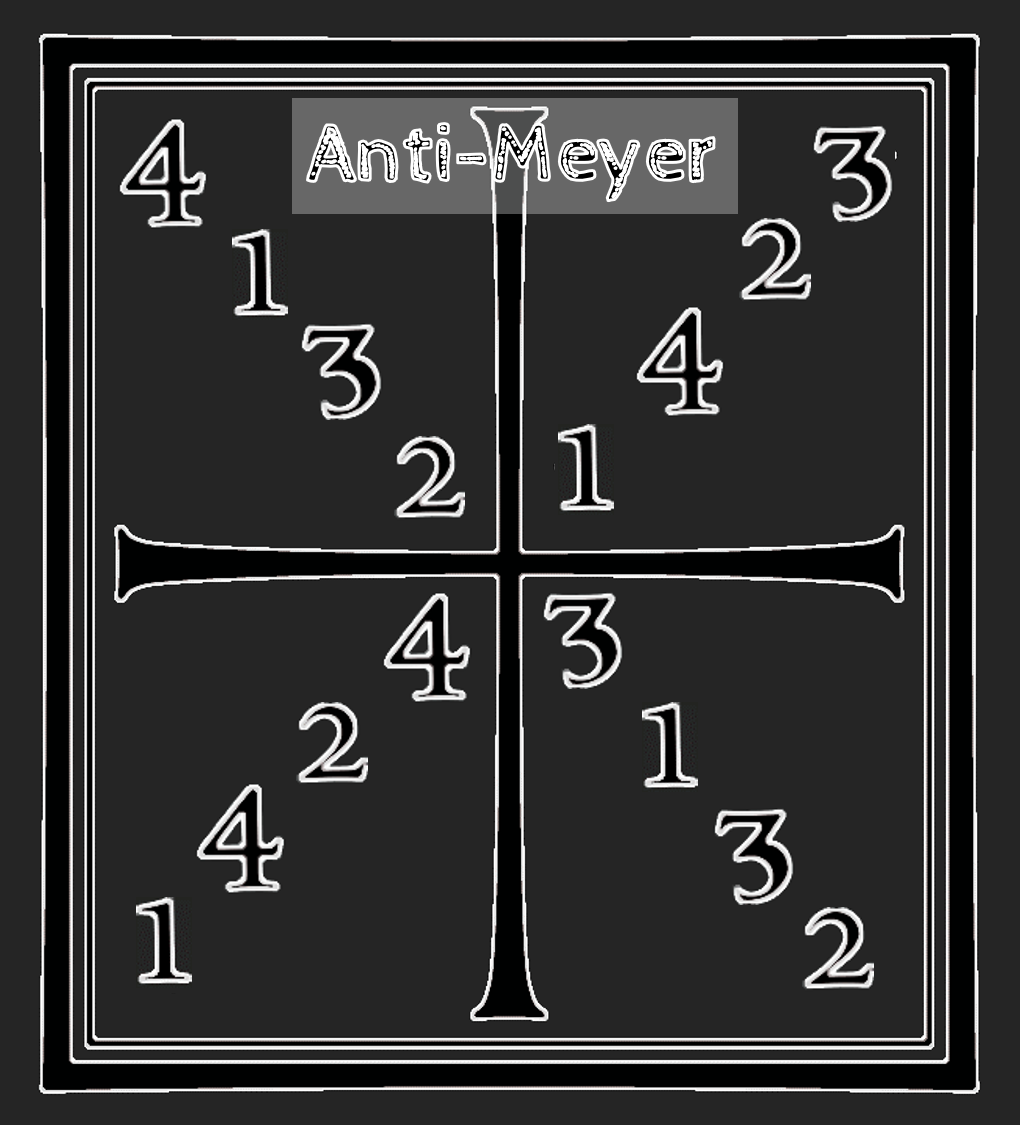
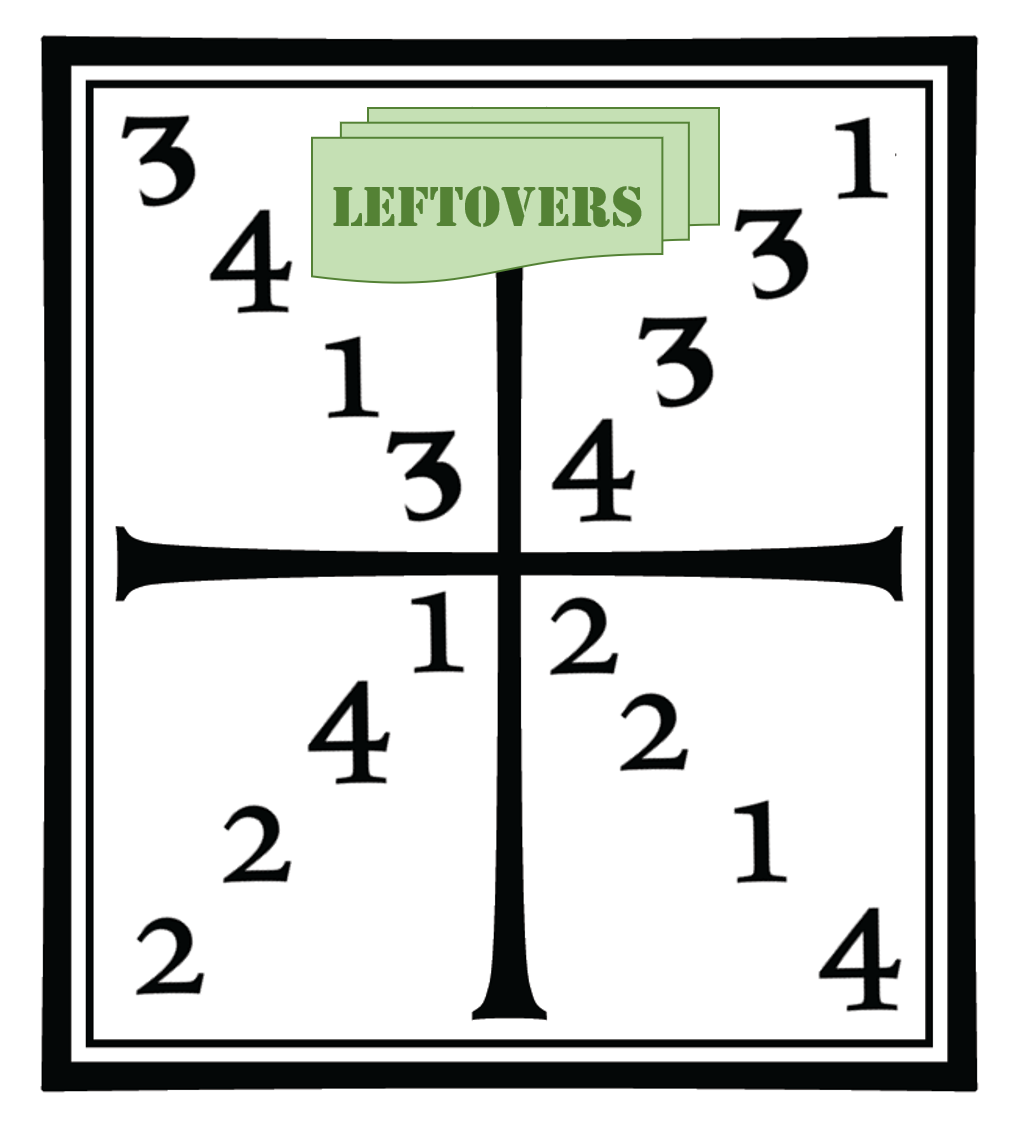
And then I took a crack at things with whatever was left over. Give them a try and see what you think.