In general you can sort modern feder designs into two categories: without fuller and with fuller. (Note that I am speaking of the modern production feder, which is a different tool serving a different purpose from the historical federschwert.)
Creating a fuller on a sword is typically used to reduce the mass of the sword, while retaining as much stiffness as possible. (You can’t make the blade stiffer by removing weight, however you can make the blade stiffer in relation to its own weight. So it won’t flex as much when you are swinging it around in the air). In a feder the goal is slightly different. Having a fuller allows you to maintain the same blade mass, but push the steel out towards the edges. This makes the edge more durable.
However, in a completely non-intuitive trick of physics, doing this actually makes the sword more likely to take a permanent set. Let’s have a look!
(If you want more background on sword stiffness, I’m already way ahead of you: What makes a sword stiff?)
Section Modulus
If you take something and bend it, you are stretching the ‘top’ and compressing the ‘bottom’. This means that the thicker the object you are bending is, the more the ‘top’ has to stretch. Which means that these regions are under a lot more stress than the center of the object.
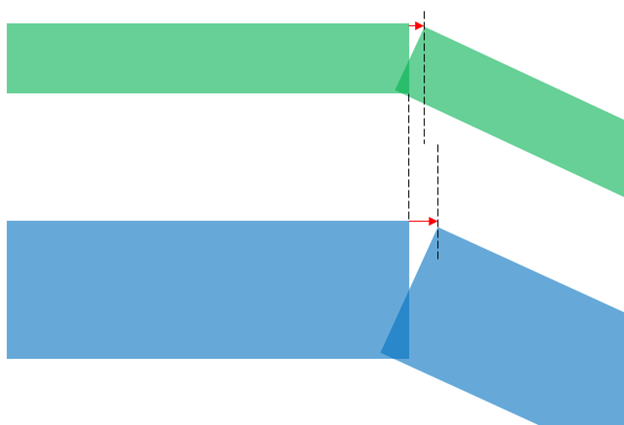
TL;DR: For the same amount of flex the thicker object will have more internal stress.
It is very true that thicker objects tend to bend less than thinner objects. And if they bend less, shouldn’t that mean that they have less stress? Sort of.
As you would know from reading my other articles on stiffness, an object’s resistance to bending is a function of its cross sectional area. This number is known as the Second Moment of Inertia (or the 2nd Moment of Area, Second Area Moment, or Area Moment of Inertia…). The higher it is, the more an object wants to resist bending. When we take both into account we get our Section Modulus.

Note that in this case we are interested in how the sword bends (aka flexes) along the flat.
Thickening the Edges
The major benefit of having a fuller on a feder is that you can bring material from the center of the blade out towards the edges, thus making it wider and better able to handle the repeated impacts we subject our swords to. So I began a simple simulation on what would happen if I took the cross section of my feder, and started digging a fuller into it and moving the material out towards the edges, all while keeping the total weight of the blade the same.
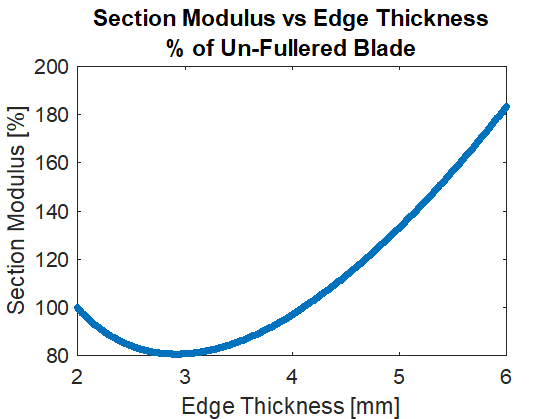
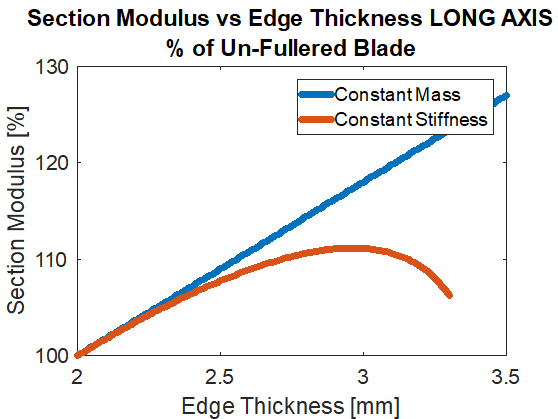
We see the Section Modulus initially decrease as we started “fuller-ifying” the blade. But then after about 4mm of edge thickness we start seeing the Section Modulus increase. At this point we have a sword with an edge twice as thick but handles just the same. (We haven’t added or removed any steel, just moved it out towards the edges).
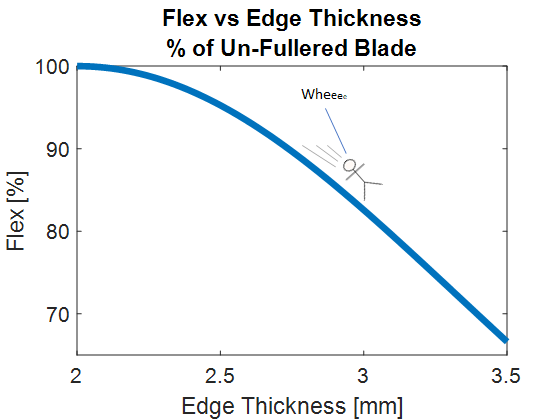
While the blade would handle the same, it would not behave the same on impact. In order to get back to break-even on the Section Modulus we would have to give up half of the sword’s flex! Sub-par.
Constant Flex
So instead of maintaining constant mass on the sword, let’s instead keep the flex the same. In order to do this we will need to take more mass out of the fuller than we add to the edge.
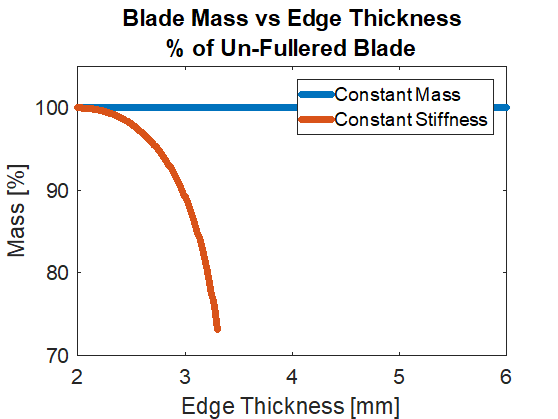
We see that as we move steel towards the edges we have to take exponentially more mass away from the fuller. This is because of the way the I-Beam is shaped, which is designed to give maximum stiffness for minimum weight. Once the sword gets to 1mm of steel in the center of the blade I cut off the calculation, as at this point we have almost cut our blade in half.
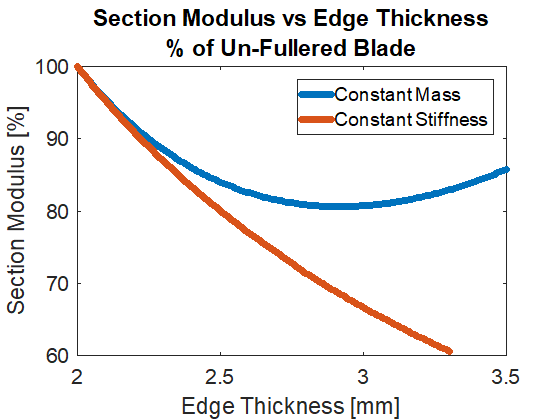
While maintaining the constant flex we see the Section Modulus plumet. By going from a 2mm to a 3mm thick edge we are increasing the maximum bending stress on the sword by almost 50%!
Conclusion
Given an equal level of blade flex, a feder with a fuller is more likely to take a set. This is because the shape drives more steel out towards the edges, and makes them wider, and thus they experience higher bending stresses when the sword flexes.
On the flipside, if the feder has wider edges the impact forces from two swords meeting are considerably lower. You don’t need any calculus to work out that going from a 2mm to a 4mm edge cuts the contact pressure in half. (Force vs Pressure)
So the question is, do you have more of an issue with your feder taking sets, or issues with your feder edge getting banged up?
Tune in for next time*, when I compare data collected from common production swords.
*next time used as a figure of speech and does not indicate a promise to have data collected in time for the next scheduled article.
Stuff For Nerds
The reference sword I used was the cross section of my Ensifer Standard Feder, produced in 2012. I measured a point 30 cm from the tip, which is about the region where we commonly see sword sets and breaks.
| Thickness | 2 mm |
| Width | 20 mm (actually 19, but 20 was a much more convenient number) |
To construct the fullered sword I used a constant width fuller of 16 mm, reasoning that it seemed about right from memory. From here the blade was thickened as the fuller was carved into it.
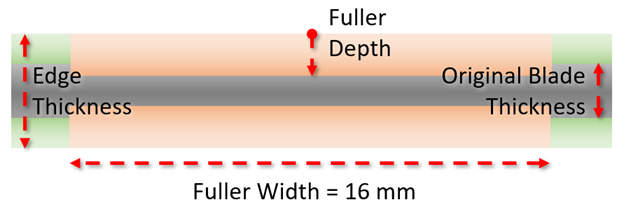
At first I thought I could plug fuller depth into a simple spreadsheet, to see how the Section Modulus changed as I moved the mass to the edge and dug in a fuller. But getting the right equation was proving elusive.
And then I tried to solve it by hand, and soon figured out why. You know a SwordSTEM article is about to get real when I have to switch from Excel to Matlab.

And after all that we get to some usable data.
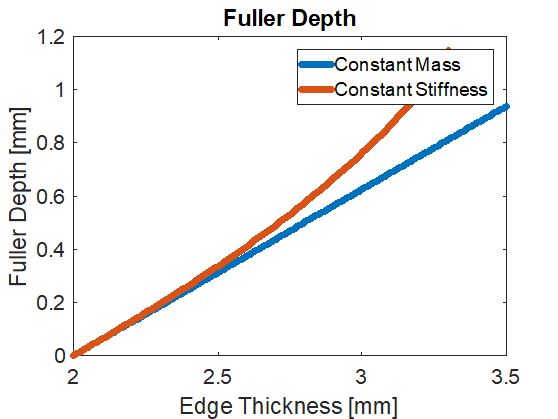
The other interesting phenomenon is that the blade will eventually start to get weaker along its strong axis. At first the blade gets stronger, as you are moving material out towards the edges. But after a certain point, the center of the blade is so thin that we start actually losing more strength than we gain.
And what about the fact that feders don’t have uniform cross sections, or the fact that feders with fullers tend to have different profiles?


