One thing wooden training weapons are associated with is being excessively stiff in the thrust. It’s common knowledge that wooden training weapons are stiff, right?
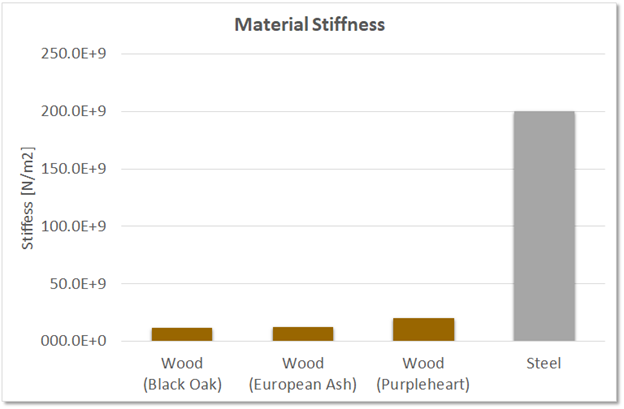
But wood is actually considerably less stiff than steel! That seems like quite the contradiction — after all, we know from firsthand experience what happens in a stiff thrust from a wooden training weapon.
Shape Matters
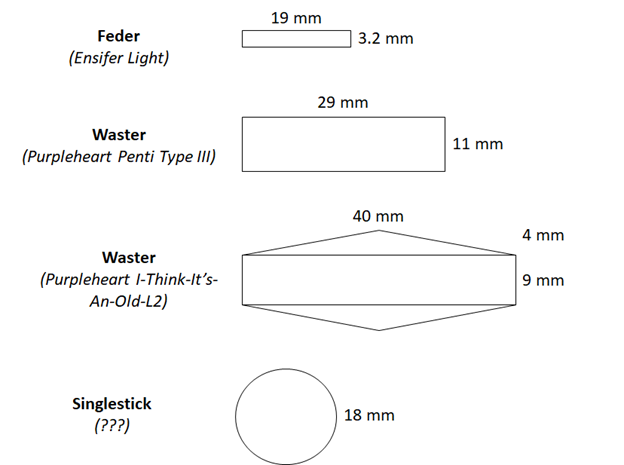
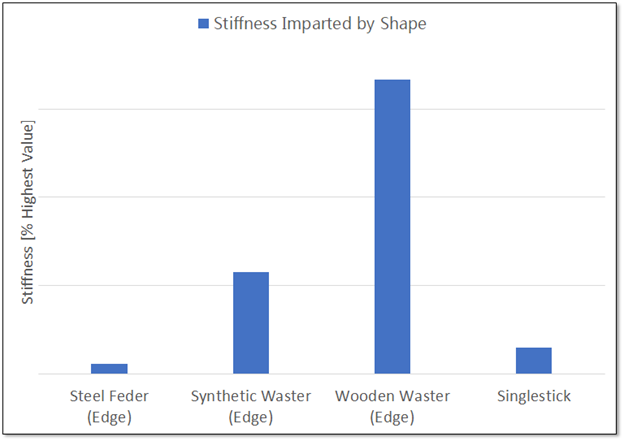
You might have also noticed that wooden training weapons tend to be much thicker than their equivalent steel training tools. A wooden waster is a ton thicker than a feder.
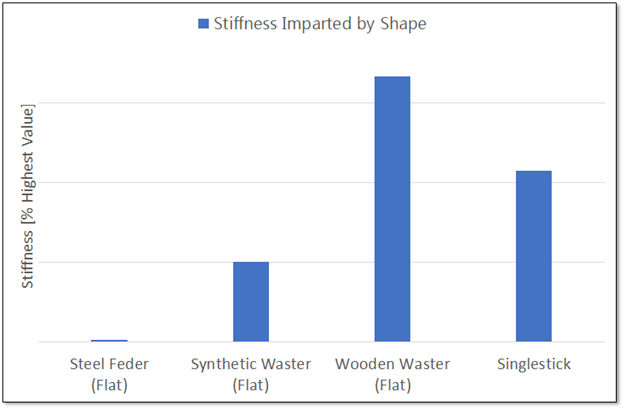
The reason that the singlestick is so dangerous in the thrust is because the stick doesn’t have a ‘flat’ to bend around. If we were to compare the edge of the feder to the singlestick we would see the difference isn’t as large.
The physical quantity that is important here is the Second Moment of Area, also known as the Second Moment of Inertia, also also known as the Area Moment of Inertia. Yes, historical German fencing masters weren’t the only ones who couldn’t get their terminology straight.
Imagine that you cut a sword in half and are looking at the cross section. The shape of this cross section determines how well it bends.
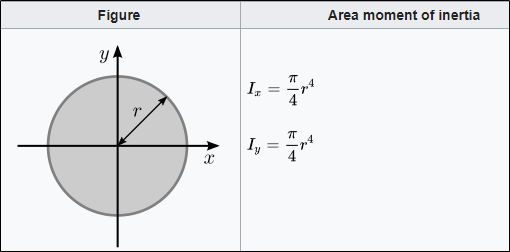
Ix and Iy denote the difficulty of bending the shape along the X and Y axis, equivalent of bending along the flat or the edge. You will notice they are the same, which makes sense, as a round stick has no ‘flat’ or ‘edge’. The physics can’t differentiate if the impact happened on ‘edge’ or not, much like most singlestick practitioners.
What you might notice is that the formula involves the radius to the power of four. This means that the stiffness of a stick is proportional to its thickness, times its thickness, times its thickness, times its thickness. Or moving from a 0.75” (1.9 cm) stick to a 1” (2.5 cm) thick stick would make it over three times as stiff!
When dealing with rectangular shapes (like swords), you have to consider if it is bending on the edge or on the flat. I won’t bore you with math, just know that the strength increases along the bending edge by a power of 3 (cubic), and linearly along the other axis. So if you make a sword twice as thick, it will be 8 times as stiff — but if you make the blade twice as wide, it is only twice as stiff in the thrust.
If you are interested in how shape affects stiffness, have a look at Wikipedia’s List of Second Moments of Area.
Material Matters
As we saw in the first graph, steel is much stiffer than wood. The overall stiffness is a combination of the stiffness due to the shape, and the stiffness due to the material. Let’s take a look at the last graph, but with the material thrown into the mix.
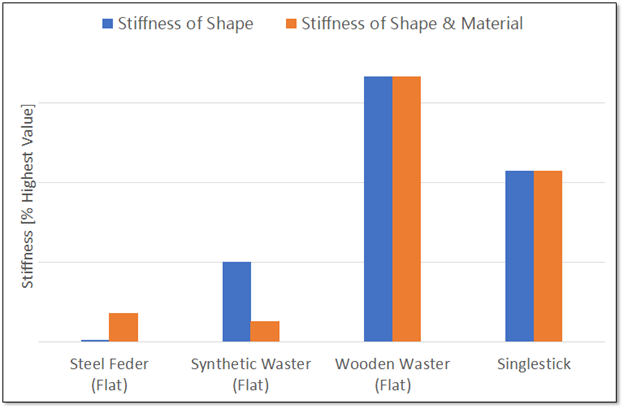
The cross section of the synthetic waster is much thicker than the feder, but once you account for the material differences between the steel and nylon, the overall stiffness of the steel feder ends up noticeably higher. The wood isn’t as stiff as the steel, but it’s just so much thicker that it doesn’t matter. That singlestick is going to thrust HARD.
Physics be damned, life isn’t all boxes
At this point you may wondering how I factored in the constant change in the blade’s cross sectional area? As you move towards the tip it becomes thinner and narrower.
The answer is: I didn’t.
Most Moment of Area calculations are done based on simplifying shapes into simple geometric ones that already have formulas. You look up these formulas in handy tables, and get a number that is an approximation.

The math to calculate this for an arbitrary shape can get ugly.
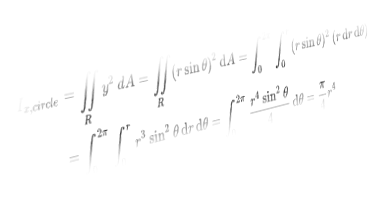
To get the full stiffness of a shape that changes over its length, we have to do crazy math that takes that other crazy math, and crazies it over the entire length. In reality at that point you have two options:
- Be a crazy mathematician.
- Create a computer model and have the computer do it.
- Just take the damn thing, bend it, and see what happens*.
So all them there fancy book-learnings only get you so far.
*This isn’t a widely known fact outside of engineering, but engineers actually tend to hate math, and find ways of getting out of it when they can.
I-Beams and Blood Grooves
A little known fact: the blood groove has a secondary purpose — to decrease the mass of the sword.
(People newer to the sword community may not understand the reference. Somehow it got popularized that fullers were ‘blood grooves’, a channel cut into the sword to allow the blood to drain from a wound and prevent suction and the sword getting stuck. This is completely ridiculous, and the mention of the term alone makes many old school practitioners want to slam heads against their keyboards.)
Let’s take a sweet prototype training sword* which is square in cross section.
*bludgeon

Like everything, it has a stiffness.
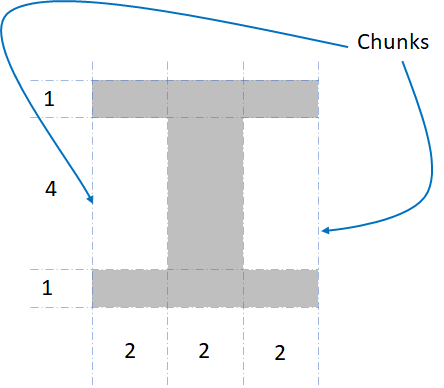
This decreases the overall mass by 44%. Any guess at how much it decreased the stiffness by?
…
Come on, guess!
…
The answer is only twenty two percent. We lost half the mass, but only about a quarter of the stiffness! This is the reason things like I-Beams and similar shapes are so common in construction–they get the best strength to weight ratio.
A sword fuller is the same thing.
Less Steel = More Stiff?
Let’s get one thing straight, a sword with a fuller is LESS stiff than a sword without one. This may be counterintuitive, having handled and swung swords around. The difference is that adding a fuller also makes the sword lighter. You effectively change the sword’s “weight-stiffness” ratio, making it seem more stiff when you are handling it and the only force it has to deal with is generated by its own weight.
But if you were to drive a hard thrust into someone with both the fullered and un-fullered blades, you could see the difference.
(This does assume that the sword is the same otherwise. If you take the steel you took out of the fuller and distribute it on the edges of the sword, it’s going to be way stiffer than the original sword.)
Torsional Bending
Most of the time when we think of swords being stiff/not stiff, we think of thrusts. But what about a cut?
When you strike on edge* you are in theory bending the sword along its strong axis, which is about 40 times as stiff as bending it along the edge. But interesting things happen when you have such a disparity between the stiffness in the two axes. Things start to twist.
So it’s entirely possible that the stiffness of the sword can make a significant difference in how hard a sword hits in a cut. Those of us who have seen high resolution freeze frame shots of swords during high intensity matches know just how crazy and seemingly impossible some of these sword bends are.
So is torsional bending something that affects how safe a sword is in a cut?
I don’t know. 🙁
But getting data on this should be something we as a community are thinking about when deciding what exactly constitutes a safe sparring simulator!
* this is the point where I get to insult the edge alignment skills of the rest of the non-singlestick people I missed earlier.
Nerd Stuff
These are the training tools I used, and the point at which I took my measurements.

These are the shapes I used to calculate my moments of inertia.