When fencing we are always trying to get the most advantageous position, be it through our reach or our ability to dominate the sword of the opposing fighter. And we actually have a cool trick to tie both of them together. But first let’s look at a little bit of geometry and physiology. Spoiler: it has to do with quarte and schielhau.
(I’m going to carry through this geometry using a somewhat artificial model–someone holding a longsword with both hands essentially on top of each other. Doing it this way makes it both simpler to understand and easier to make diagrams.)
Blade Crossings
If you are going to constrain your opponent’s blade and thrust forward, there are many things that will help you. Things like strong/weak of the blade are important, as well as basic lever actions which are fairly intuitive. What I want to talk about is:
- Moving your hand(s) further across the center.
- Moving your hand(s) higher.
Both of these things help you get a better mechanical advantage over your adversary, but have a natural limit. If you cross over the centerline too strongly you take the sword out of your body’s centerline, and lose structure. The way to avoid this is to turn your body to match the new position, which then creates its own tactical problems.
Moving your hands (and thus your hilt) higher will, in most cases, only do good things for the leverage on the blade. It will not always do good things for your body position.
There is a natural mechanical limit to how far you can raise your hands, and a tactical limit to how far you can turn your body against your opponent’s action. Keep that in mind as we go on to our next problem.
(Some people may notice that I plagiarized most of this section from my previous Geometry Grab Bag article. But probably not too many, if my page-view analytics are to be believed.)
Geometry and Range
It’s pretty well known that the lower you go, the more range you lose.
However this isn’t completely accurate. More specifically it is going lower than your shoulder that loses you range. This is why when targeting the lower openings it is advantageous to drop the stance, minimizing the amount of range you lose. Or why a shorter fighter is going to be less disadvantaged going low (double negative on purpose).
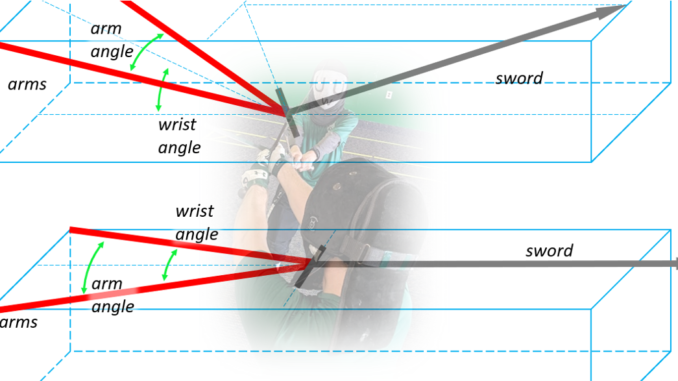
But enough about that. Let’s talk about wrist angles (again). The natural position of holding the sword introduces an angle at the wrist. Different methods of holding will produce more or less angle, but it’s pretty hard to get rid of as we discussed in the structure section above. The following shows how much you do lose based on the wrist position.
We can’t completely eliminate this without adopting a hyper-specialized grip – which some rapier systems do. But in most situations it’s a case of minimizing rather than eliminating the problem.
The same situation also occurs when looking at shoulder position. Have a look at a person holding a sword with two hands, there is an angle formed between the two arms. Simply by extending an arm straight out from the shoulder we see an improvement in range, because we were able to eliminate the angle. (This is different from any extra reach you can gain from rotating the body.)
The Hacks
So, we have two angles that are causing us grief. And what do we do about it? Like any two problems they are easier to forget if you can cram them both in the same drawer.
The first angle, the wrist angle (between the sword and arm), is located in the vertical plane. The second angle, the arm angle (between the two arms) is located in the horizontal plane. However if we were to rotate the sword so that both the arm angle and the wrist angle are in the same plane, then we only have to get the angle ‘penalty’ affecting our reach once.
Z-Axis Rotation
I call the rotation of a sword about its long edge “Z-Axis Rotation”, because it is as descriptive as it is cool sounding. When describing stuff, mathematicians have their go-to algebra symbol: ‘X’. When they need something else, the go-to is ‘Y’. Using those great 1st grade pattern recognition skills, I’m sure you are way ahead of me in guessing Thing 3 is slapped with the ‘Z’ label.
So what do I mean by Z-Axis rotation? You have three ways you can rotate a sword. First is the obvious cutting plane, let’s call it X. Then you have the flat cutting plane, which we’ll call Y. The final way to rotate the blade is along the length of the blade, which becomes Z.
Going Way Back To Structure
The z-axis rotation of the blade not only helps with the reach problem, it can help with the constraining problem. We’ve identified that holding the sword in a conventional extended position we can only achieve two out of three:
- Body structure maintained.
- Sword towards opponent.
- Crossing centerline.
By rotating the sword around the ‘Z-Axis’ we can achieve a larger centerline cross, and higher hand positions while mitigating the negative structural effects.

While this does increase our ability to displace a blade, it does have some possible consequences with regards to reach (which was the focus of the last section). Naturally if you are using the z-axis rotation to drive your sword further offline you are going to be shorting yourself on reach.
Summary
So, why did I say that shiel and quarte are the same thing? Because they are both taking advantage of this z-axis rotation principle.
Now, you may ask why the shiel has the blade oriented vertically whereas in quarte the blade is horizontal. Normally if I bring up a question in the summary it’s to say “I don’t know” and run away, but this time I do have an answer to this!
In quarte you are doing one thing, the rotation of the arm 90 degrees to facilitate the movement. In a schielhau you are actually doing two things: 1) perform a grip switch which moves the sword 90 degrees, 2) rotation of the arms 90 degrees. If, with a longsword, you only perform the 90 degree arm rotation you will end up with the crossguard horizontal – just like you see when tournament fighters are doing a winding on the blade to complete their thrusts.
So that wraps this up nicely. Knowing the geometry involved doesn’t really change anything about how we use these types of motions, based on the historical sources and modern practice we have figured out pretty well. But now you know why!

