
In writing an article about thrusting force, I’ve come to realize that there are some misconceptions about the relationship between force and momentum when it comes to delivering a thrust. This is specifically talking about thrusts, but the concepts of Momentum and Impulse are further elaborated in Impact Impulse and Momentum, so I suggest you check that out as well.
Weight vs Impact Force
A simple example to start. Pick your favorite hard cover HEMA manual, the bigger the better. In my case let’s use the Second Edition of Michael Greer’s translation of Thibault, weighing in at 2.7 pounds. Now take the book and rest it on your foot.

I used the term ‘weighing in’ very deliberately. Weight is an expression of how much the force of gravity is pulling on something. This book weighs 2.7 pounds (in imperial) or 12.0 newtons (in smart people units). Its mass is 1.2 kilograms (metric) or 0.084 slugs* (imperial).
Why is that important? Well, to truly understand bring that same book up to eye level…
And then drop it on your foot.

They key thing to grasp is that this book weighs the same in both cases. But we can obviously tell that they didn’t exactly exert the same force on your foot.
*Slugs is actually the proper unit of mass in imperial, with pounds actually being a unit of force. So the next time someone tries to act smart douchey by correcting you on the difference between force/mass, you can tell them that they are in fact doing it wrong.

Accelerating Force vs Impact Force
The key is the distance that the force is applied over. Let’s consider another example, one where no one gets hurt.

If you take an egg and drop it onto your kitchen floor you likely have a mess to clean up. (This is one of the best reasons to own a dog.) If you instead drop that egg on to a super comfy pillow there is a good chance that you can end up with the egg intact.
The difference is that the floor stops the egg all at once, whereas the the pillow stops it slowly, over a longer period of time.

Similarly you can think of a car. You can go hard on the accelerator pedal for a short amount of time to get up to speed, or go light on the pedal for a longer time to reach the same speed. You can crash into a barn full of hay and experience a large force for a short amount of time, or you can crash into a concrete wall and experience a really large force for a really short amount of time.
(To be precise and satisfy the quibblers* I will clarify. Crashing into the barn produces a large negative acceleration (deceleration) as you quickly go from moving to stopped. This is because the barn/stuff in the barn are exerting a large force on your car. The car hitting a concrete wall instigates an even larger negative acceleration by exerting an even larger force on your car, meaning it goes from moving to stopped in an even shorter period of time.)
* my editor.
On to Swords
This physics principle is what can make people confused about what numbers mean what, when talking about thrust force. Let’s look at the common statement:
“It only takes 4 ounces of pressure for a thrust to penetrate the skin.”
First of it’s completely wrong because it makes no sense. Ounces is a unit of force, not pressure. (I’ve already written an article on Force vs Pressure.)
“It only takes 4 ounces of pressure force for a thrust to penetrate the skin.”
Ok, now that at least makes sense from a physics point of view*.
If this claim is correct it means if I take blade weighing 4 ounces, and balance it tip-down on any part of my body it will stab into me. Gravity is exerting the 4 oz it needs to do the job. If I took a 3 ounce blade and did the same thing I would be perfectly safe.
But if I drop the 3 ounce knife on to something it is going to end up exerting far more force on the target.

* It’s just completely wrong from a being wrong point of view. But I’ll elaborate more on that in the future.
And Lunges
Let’s say you want to know how much force it takes to thrust a sword through your carefully calibrated choice of test medium*. You first, as a responsible and diligent scientist, calibrate exactly how hard you are pushing the sword. Select a magic number, like 5 pounds, and thrust at the target using said force.
*whatever you had lying around.
Voila! The sword goes through! Clearly 5 lbs was all it took.
But no! That’s not how it works. If you don’t remember, you can drop another book on your foot to jog your memory. You might have only been pushing on the sword with 5 pounds, but the contact force between you and the target would have been much, much higher! (It’s the same as dropping a 5 pound book on your foot and placing a 5 pound book on your foot.)
How much higher is very hard to say. It depends on how long you had to accelerate the sword, and how resistive the material you were thrusting into was. For now it’s sufficient to know that 5 pounds is very much not the real number.
You Promised Me Swords and Tanks
I did.
Our scenario plays out as follows.
- You have a sword
- The sword is magic and won’t break or flex on you.
- You can only apply 4 oz of force to the sword.
- You have as much time/distance as you need to get the sword up to speed, pushing a steady 4 oz of force on it.
- We don’t have wind resistance, a maximum running speed, or anything else that would make this realistic.

Turns out that you need quite a bit of distance to get that blade up to speed, a 50 km run up. But this will give you enough speed to penetrate tank armor by only thrusting with 4 ounces of force!
Stuff For Nerds
Accelerating Force, 4 oz = 1.11 N
Acceleration = 1.1 N / 1.4 kg = 0.785 m/s2
Thickness of WWII Panther 2 tank on the side: ~40mm -> 1.6 inches [2]
Modeling the Sword as a hardened steel shell core, it requires about 40e3 FT lbs/in^2 of energy/diameter^2 to penetrate.[3] (A tank shell is definitely not the same as a sword, but somehow I couldn’t find scholarly articles about stabbing swords into tanks.)
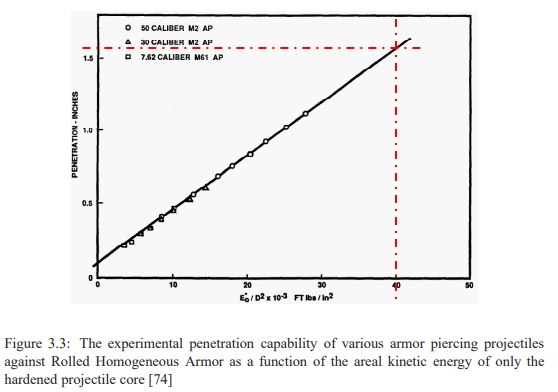
Effective Penetration Diameter = 1 inch. (A reasonable cross section of a medieval sword which makes the math simple)
Kinetic Energy = 40e3 FT lbs/in^2 * (1 in * 1 in) = 40e3 FT lbs = 54e3 J. (Note that the formula used diameter squared, not surface area).
Required Impact Speed = sqrt(2 * 54e3 J / 1.4 kg) = 280 m/s
Time = (280 m/s) / (0.785 m/s2) = 357 s ~= 6 minutes
Distance = 280 m/s * 357s / 2 = 50 km
Bibliography
[1] Franklin, S. (2018). Force vs Pressure – Sword STEM. [online] Swordstem.com. Available at: https://swordstem.com/2018/04/26/force-vs-pressure/
[2] Wikipedia!! https://en.m.wikipedia.org/wiki/Panther_tank
[3] Deniz, Tansel (2010). Balistic Penetration of Hardened Steel Plates. https://etd.lib.metu.edu.tr/upload/12613534/index.pdf

