That’s right, you heard me. To clarify, I don’t mean that you can not throw a zwerch horizontally, I am saying that you can not generate a cutting plane. Not because of my interpretation, but because of geometry.
But before we begin, we need to clarify what exactly a zwerchau is. So, for the purpose of this article, I will consider the zwerchau to be:
- A strike that is more horizontal than vertical.
- Has the arm below the sword (instead of inline, like a normal horizontal cut)

If you disagree with either of these, you might as well stop reading. 😉
Diagrams
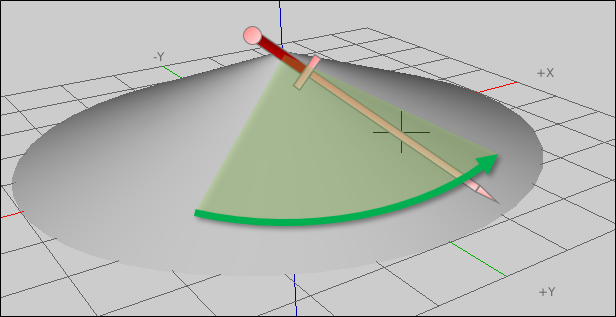
People are complicated, in many ways[citation needed]. Keeping track of all the body’s geometry is difficult, which is why we explain things with simplified models. Based on the above points about the zwerch, it will look something like this:
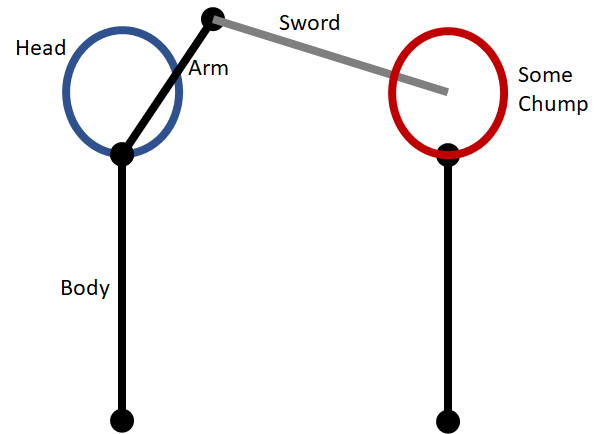
Because of the two restrictions* you are constrained to keep your sword tip lower than your hands.
*I know that it’s theoretically possible to do something like: bend your arms, tuck your sword in to your chest, spin, and still be within my two rules. It’s also really stupid. You’ll find you get further in life if you aren’t stupid.
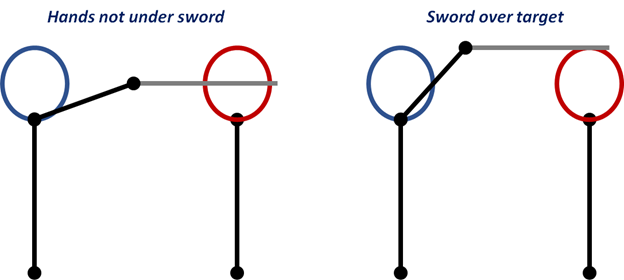
Though this model is simple, we can even go simpler. It was only necessary to include the height of the head & shoulder to show that the sword tip must be lower than the hilt. Once we know that we can produce:
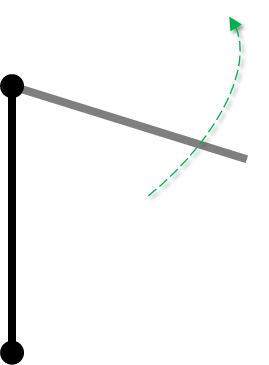
Umbrella Zwerch
Umbrella zwerch is the term I use to describe a zwerchau in which the tip remains at the same elevation through its arc. This is because the shape that the blade traverses forms a cone over the head, a.k.a. an umbrella. I know umbrellas seem kind of safe, after all they shield us from things coming down towards our head. But they also aren’t optimized for cutting.
Curves vs Lines
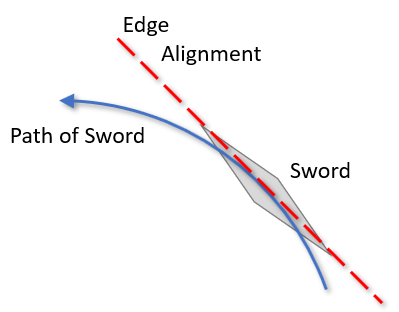
A tangent line of a path can be thought of as exactly where something is pointed at this exact moment in time. In a straight cut the tangent line and the path of the sword are exactly in line. Two straight lines on top of each other. But with a circle it doesn’t work. By definition the tangent is straight, and the circle is curved; therefore a tangent can never run parallel to a circle. It only touches it at a single point.
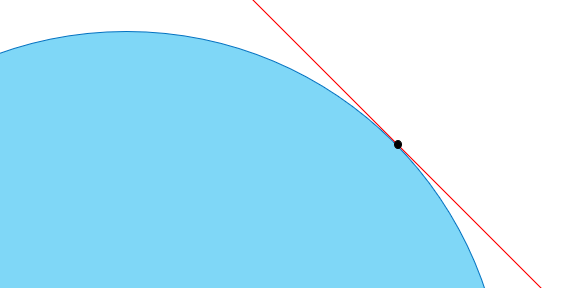
Because of this the edge alignment of the sword can never actually match the path of the sword traveling on a curve. And traveling on a curve is exactly what the umbrella zwerch does. Which means that at any given moment in time, the umbrella zwerch can not have perfect edge alignment.
Cutting Planes
To be effective at cutting we need the sword’s edge in alignment with its direction of motion. This means that the sword would trace a disk in space, rather than a cone like the umbrella zwerch. So how can we get a cutting plane for our zwerchau, while still hitting the target? Have the cut be delivered on a slight angle.
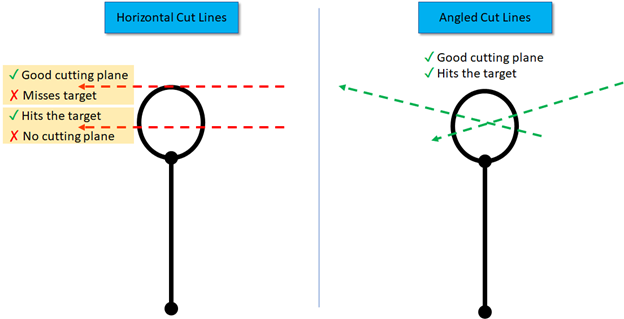
How much of an angle? Well that would depend on where your hands are, and where your tip is. The larger the difference, the more angle you need! In many cases the angle is very slight, someone watching from the sidelines might not even notice. The body has a lot of articulation, and you can move the plane’s center of rotation all over the place. The important part is that the person delivering the cut moves their sword along a plane, rather than an umbrella a cone.
The Big Exception
There is one significant exception to what I have just said: I assume that the top of your head is about the same height as the top of your opponent’s. And this just isn’t always the case.

If you are shorter than your opponent you can have the sword tip and your hands at the same height, which completely invalidates the “there us no horizontal zwerch cutting plane” thing.
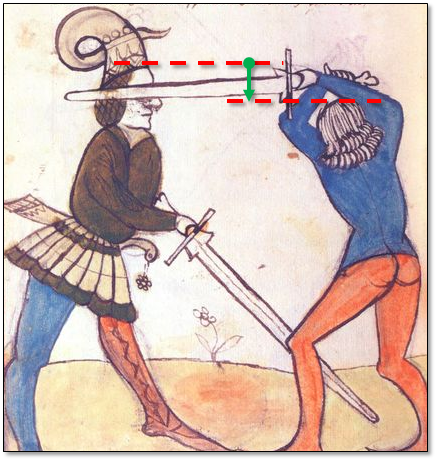
Conclusion
First of all, we should all be aware that the zwerchau does many things in addition to cutting*. If you are just intending to get your blade out there to intercept the opponent’s blade do you really care about having a good cutting place? Probably not. If you are strong, have a very sharp sword, and swing very fast, can you get through a tatami mat with an umbrella zwerch? I can assure you that the answer is yes.
What you do with the angle is going to depend on your tactical context, this isn’t an article about technique. It is an article about geometry. But you shouldn’t base your zwerchau mechanics on a mathematically impossible cutting plane!
*assuming you can actually get your zwerch to cut in the first place. :p
Edit: Post Script
I originally wanted to keep this simple, but there are two other ways to get a cutting plane at head height that fall in line with this. My assumption was they were intuitive enough that I didn’t need to mention them, but no one wants to give me a break.
1) Change the cutting plane of the sword so that it is high behind you, and low in front of you.
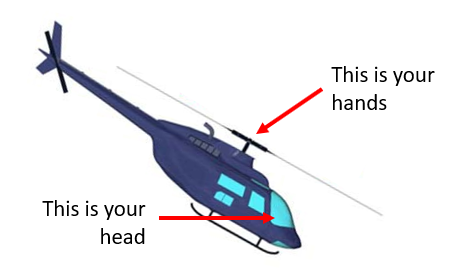
2) Lower your height so that your target is at the elevation of your hands. This can be accomplished by bending the legs or by lengthening your stance.


