
In Salvator Fabris’ 1606 treatise on rapier, he dedicates an entire chapter on the subject of flinging the sword and in-depth discussion of why this is bad [1]. In the Vienna Anonymous, a student’s gloss of Fabris from 1614, it is apparently such a bad practice that in a 14-point list of things to do to fence correctly, it is mentioned twice as a thing to not do, ever [2]. So, hypothetically, we all understand that flinging is a thing we shouldn’t do because the books tell us so. And just saying “I’m gonna fling my sword” sounds bad too. But what is flinging? And why is it poor form?
This discussion is primarily going to be concerned with the thrusting action – but the idea of wildly flinging the sword is as applicable to cuts as well.

First off, what exactly is flinging the sword? A fling is a jabbing forward of the sword, often in a wild motion, and may be done with motion of the feet or body. It is not a controlled thrust and it does not follow the proper ordering of hand-body-foot to lunge.
There are many ways one can fling the sword. Examples of flings are:
- Leaping forward with both feet,
- Throwing the sword forward into a hyperextension of the elbow.
- Retracting the sword arm and lurching it forward (often done after throwing it forward as in the second point).
- Casting the sword in a circle as if one were trying to throw a haymaker with the sword.
Fabris describes in greater detail the reasons why flinging is bad in Chapter 6 of Lo Schermo – we’ll get to those in a bit.
So, why do n00bs fling the sword? Fabris says that n00bs fling the sword because they believe it gives them more momentum. In a narrow sense the n00b is correct that moving a mass (the sword) with more velocity imparts more momentum to the mass since momentum equals mass multiplied by the velocity. And if the sword moves faster, it’ll just get there faster, right?

However, the n00b is making a few mistakes of physical thinking. Let’s begin by focusing on the mistake of merely increasing the speed of the sword.
Some physics
`Momentum in physics is a vector quantity. Let’s look at the equation:
![]()
P is the momentum. M is the mass. V is the velocity. The P and V are bolded (and have arrows above them) because they are the vectors in this equation. M is not in bold because mass is a scalar quantity – that means it is only defined by a single value, how much stuff is in there, which is measured in kilograms.
A vector is comprised of both a magnitude (how big it is) and a direction (where it’s going). Velocity is a vector, but speed is not. Speed only tells you how fast something is going. But velocity tells you how fast something is going and WHERE it is going.
To say I am going somewhere at 35 miles per hour says nothing about where I am going. My speed is a scalar quantity which means it is defined only by a single value.
If I say I am traveling 35 miles per hour in the North direction, now I am describing a vector quantity. I’ve told you where I am going and what direction I am going in.
So, the n00b’s first mistake is assuming that increasing the speed of their weapon automatically means increasing the desired momentum. The direction of the applied speed is just as important. If the increased speed is going in a direction that we don’t want it to go, the n00b may end up decreasing their desired momentum!
Thus, our first observation is that trying to increase the raw value of the speed, if done in the wrong direction, does not equate to an increase in the desired momentum. The direction matters.
So, just going faster doesn’t always increase desired momentum, what now?
Coming back to fencing, the n00b is trying to move the tip of their sword from one point in space to another. Let’s simplify the problem by assuming they are trying to move their sword in a straight line.
In Euclidean geometry, the shortest distance between two points is the straight line. And guess what? That straight line is also a vector! That quantity is comprised of a magnitude, the distance between the two points, and the direction needed to get from one to the other.
Now, here is where things get complicated. The desired resultant motion is linear – moving the tip of the sword forward. Yet, every joint in the human body (except the mandible) is rotational. That is, the individual joints of the human body move in arcs, not straight lines.
Thus, the essential problem becomes quite a challenge for the n00b to figure out. The act of planning, and executing, a motion that is fundamentally linear with rotational joints is not a trivial one. This is because rotational motion traverses fixed arcs that do not change their radial lengths.
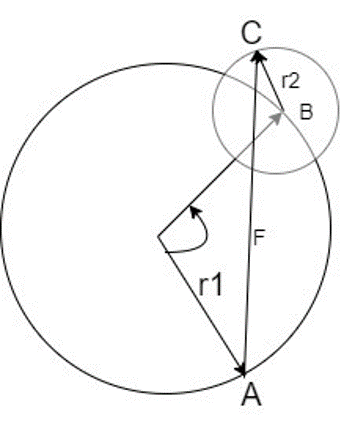
Think of a simple circle and its circumference. No matter where you are on the circle, the distance from the circumference to the center of the circle is constant. If you want to end up somewhere outside or inside the circle, and all you can do is rotate, then you must add another rotating arm.
Here is a drawing to illustrate this. To move from points A to C (a linear movement shown by line F), the radius, r1, must move along an arc from point A to B. Then, the radius of the second circle, r2, must move to the final point C. Two rotational movement joints to achieve one linear displacement!
This is a pretty stripped down view of human motion but it gives us a glimpse at the underlying challenges of kinesiology. Look at this baseball player – think of the movement necessary to throw the baseball. Which circles in the right arm correspond to which of the radiuses in Figure 5 needed to throw the ball?

To add more complication, there may be multiple paths to the same destination using the same set of joints. In the example below, this robotic arm with 2 joints is trying to move the clamp from the blue dot to the red dot. There are two paths it could take to get there – but which one is the best one? [5]
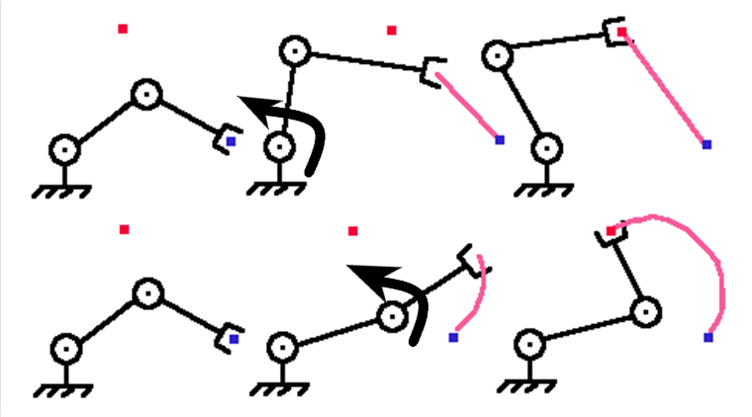
Looking at Figure 6, the top robot traverses a straight-line path. The bottom robot traverses an arced path. The top robot is ideal for moving objects with substantial mass because:
- Its net velocity vector is moving in a straight line
- The vector is easy to control as it requires only small alterations in the rotation of the joint to achieve the desired velocity.
- This means it can be started, stopped or change direction with smaller corrections
The bottom robot will have a greater speed as it moves to the destination. But, consider that as its speed is speed is larger, it will require greater joint counter-rotation in order to stop it precisely where it wants. This can cause the robot arm to overshoot if applied too late, or to stop too soon if applied too early.
Next if the arm was stopped immediately at the red dot while the robotic arm was still moving – the joint would come to an abrupt stop, but the end of the arm would still be moving and would wobble about the red dot. A sword flung forward into a hyperextended joint does the same thing.
In fencing, we are trying to solve these types of problems. Choosing the right path is part of what separates skilled fencers from n00bs. Whatever path the n00b chooses to take when they fling the sword is not necessarily incorrect – they achieve the desired outcome, which is to move the point forward. Of course, one could also argue that moving along the two legs of a right triangle also arrives at the desired destination from A to B… but it’s obviously a shorter path to just move along the hypotenuse.
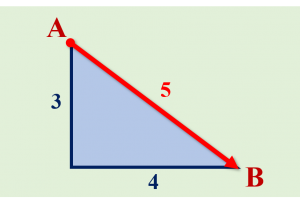
So, if the sword is flung then the n00b may not be taking the best path to get their sword in the straight line from point A to point B. Fabris remarks,
“Such flinging would not be too likely to hit the designated target because of the uncontrollable movement of the point of the sword. Also, if such a jab is executed during a lunge, the sword and the arm may fall out of line, giving the opponent prime opportunity to strike.” [1, p.8]
The very act of flinging is a lack of control of both the direction the sword is traveling and its speed. In other words, it’s harder to hit the target. The extra momentum they think they are giving their sword is wasted moving the sword in an unnecessary direction, or at an uncontrollable speed, or both. And, once that extra momentum is expended, the n00b must retract in order to fling again as all the energy available in their rotational joints is expended once fully committed.
Fabris says about this,
“If you fling the sword arm, you cannot fling it again without first withdrawing it, which creates such a long tempo that the opponent can not only wound during the first jab, but also while you withdraw your arm.” [1, p.8]
Because all motion takes time, this extra motion, equals wasted time. And, in fencing, time is precious. In fact, Fabris writes in Chapter 6 that the flung sword actions can be easily defeated by other sub-optimal actions, such as simple parries. Indeed, Fabris remarks that two-tempi actions (parry-riposte) are quite feasible against jabs and flung sword [1, p.8].
So, now the n00b needs to ask the following questions:
- If flinging the sword doesn’t impart more momentum, how should the sword come forward?
- How does one figure out achieving linear motion with rotational axes?
- In short, how does one thrust without flinging?
We shall explore the answers to these questions in Part 2.
References
- Lo Schermo, overo Scienza d’Arme, Salvator Fabris, 1606. Trans. Tom Leoni 2005
- Vienna Anonymous, 1614. Trans. Tom Leoni 2019
- Rapier (missile), Retrieved Wikipedia 2020
- Anatomy and Physiology, Retrieved OpenStax 2020
- Robot Arms Tutorial, Retrieved Society of Robots 2020
- My calculator, Retrieved 2020
- Pitcher (baseball). Retrieved Wikipedia 2020

