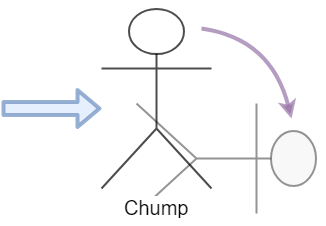
If you do enough physics, breaking a force down to its vector components becomes almost second nature, like basic arithmetic. It is something that allows you to understand what is happening around you a little bit better, oftimes changing the way you look at the world.
But I’m guessing most people reading this don’t know, and probably don’t care*, about what the difference between a vector and a scalar is. Trust me, it can be a helpful tool for learning to beat people up.
*yet.
Scalar
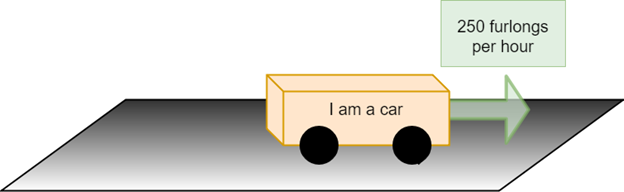
A scalar is simply how much of *something* you have. I can use a car as a simple example, and I get to break out my clip art that people seem to enjoy.

Now let’s say the car moves forward. It has a certain speed.
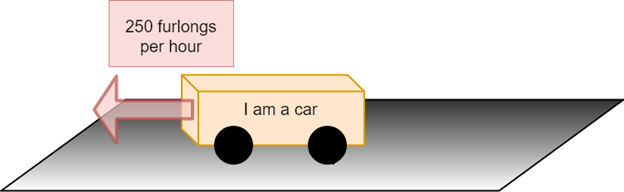
The car can also go the other way with the same speed.
As a driver, you usually only think in terms of speed. You’ve also probably heard the term velocity. Is that just fancy science talk?
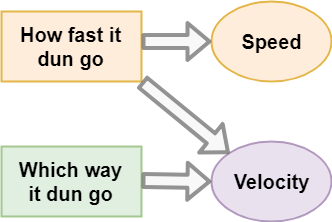
A lot of the time, we take direction for granted and just assume it. Unfortunately, that doesn’t really help when you are doing physics calculations, you need a bit more rigorous approach. Speed gets your car moving in the garage first thing in the morning. Velocity will tell you if you were accidentally in the wrong gear when you hit the pedal.
Direction
Image that you receive $100 for services rendered*. $100 is a scalar, it is the number of dollars.
Now if we add a direction to it, it becomes a vector. +$100 is you receiving one hundred dollars. -$100 would be losing one hundred dollars, lets say to services rendered to you.
The direction is relative to some reference frame. In this case you are the reference frame, positive values indicate that the cash is coming in to you. Negative values indicates that it is going away from you.

The funny thing is that the direction is always relative. If you look at it from the other person’s point of view, the directions are opposite. You getting money is a negative direction for them. This is why when working with vectors it’s always important to consider a Reference Frame. Or in other words, what the direction is in relation to.
Specifying the reference frame is of vital importance when doing math and physics. However, for the purpose of this article, I’ll just kind of let it slide.
* this can function as a personal rorschach test. What did you think of first?
Multi-Dimensions
The examples I have given so far are what you would call one-dimensional vectors. You can be either going forward or backwards.
Unfortunately, we live in a three dimensional world — or possibly significantly more depending on what kind of physics you are doing. I’ll do what every entry level physics class does, and show you two dimensional examples, and trust you can figure three dimensional out on your own.
Let’s say you know that you have to get somewhere 10 steps away. But you don’t know which direction to go in!
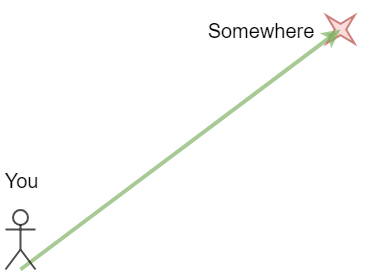
What if someone told you “Eight steps east and six steps north”? That would probably make things a lot simpler.
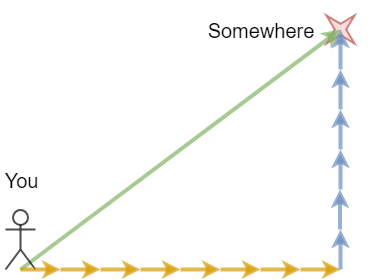
We can break down the location into components. We might specify this location as “8 m East and 6 m North”. The important thing is you can do this sort of thing with all vectors. Break it up into its component forces. And it does actually help you with martial arts.
Force Vectors
Let’s push a box.
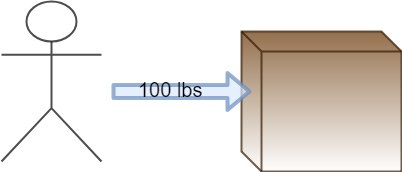
Remember when we talked about vectors earlier? They can be broken down into components. Let’s break this force vector into components, one component force in the direction we want to go, and one perpendicular to that.
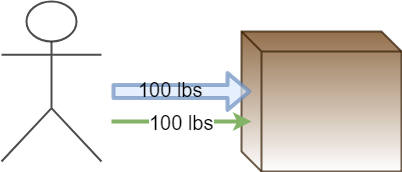
That was fairly straightforward. We push with 100 pounds of force, and we get all 100 lbs of force going in the direction we want. But let’s say we want to push the box even faster, so we lean over a little bit to get a better leverage, and push harder.
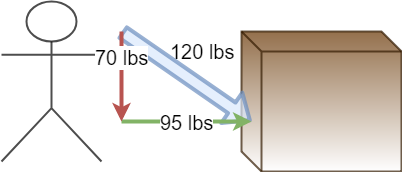
You now feel like you are pushing much harder. That’s because you are! You increased your force production by 20%. But the box goes slower….
This is because you increased the total force, but the component of force moving the box forward didn’t go up at all. Even worse you now added a component of force driving the box into the floor, increasing the friction.
This is a physics explanation for what martial artists have known intuitively for a long time. The way you apply force is often more important than how much you apply.
(Of course the corollary to this is that even if you aren’t pushing at completely the correct angle, if you apply enough force you can still get it done. 70% efficiency of 200 lbs is still more than 100% efficiency of 100 lbs!)
Throwing people is more fun than pushing boxes.
Now we want to push someone over.
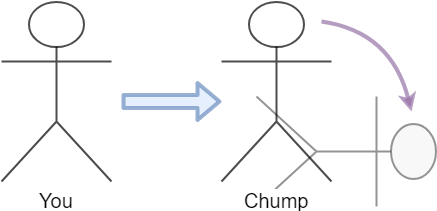
Unfortunately, unless you are a ki fighting master, people usually don’t just co-operate and fall over. They resist and it takes some work on your part. So you decide to tower up over your opponent and throw your body weight into them.
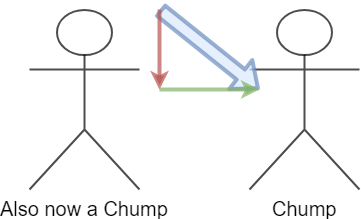
We just wasted a bunch of that force pushing them into the ground, when we want to be pushing them over. (Unless you are strong enough to just crush them. At that point feel free to do this.)
It gets even worse though! The force your opponent is using to resist you is coming from their contact with the ground. If you push down, you strengthen their connection to the ground, ensuring they can bring their full force to bear on you. While you may feel like you are pushing much harder, you are actually being much less effective.
But what if you push up? At this point you are also losing force, are you not?
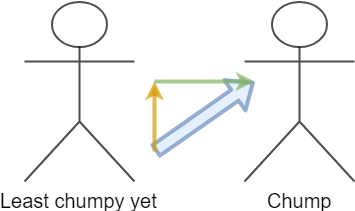
Yes, but it’s important to remember what I said in the previous example. Your opponent resists through their contact with the ground. By having a component of your force act in the vertical direction you are ‘picking them up’ a little bit, and robbing them of stability. This means you need significantly less force to push them over.
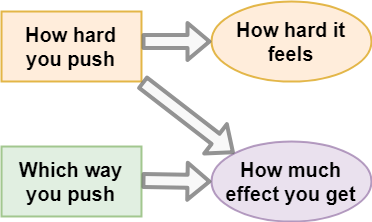
This is where force vector thinking can come in handy. Don’t just think of how hard you are pushing (a scalar), think of which direction each of the force components are acting (vector).
Footwork
You are fighting and your opponent is being a wuss and not just walking into your measure. You have to suffer the indignity of taking a step towards them to strike.
Because very few of us wear jetpacks when we fight, to move forward you have to press on the ground with your foot, have the ground press back at you, and that force moves you forward.
The force you push on the ground with is more or less in line with your leg.
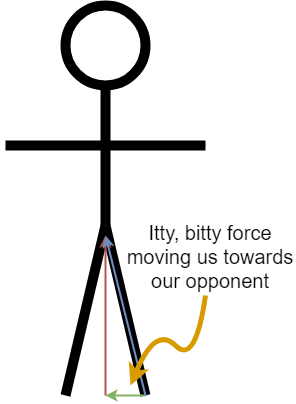
If you are in a high stance, most of that force is going straight up. Not a lot of it is actually moving you forward.
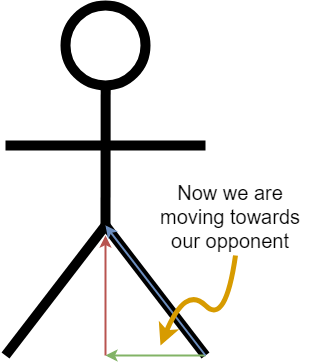
By lowering your stance, you get a much higher component of your force moving towards your opponent. But you also get a lower component holding you upright. This means that a lot more of your total force is translated into moving you forward, but a lot less is used to hold your body weight up. This is why lower stances tax your legs more.
Think about this the next time you are doing footwork drills. What direction are you pushing on the ground, and what does that do for your body? Like everything, it’s a trade-off. If you are completely upright, you won’t be able to move effectively in any direction. If you go too low you are wasting too much effort supporting your body weight, and your legs must over-work.
If only we were all stick figures
It’s super easy to draw force vectors on stick figures. But people are a little more complicated. Though these are laws of physics and are always applicable, the geometry of the body may make things work differently than you would expect from my stick figure drawings (and you trusted me!).
So the moral of the story is that when thinking about how you move, how you throw, or how you are accelerating the sword in space, take a second to think about how you are applying force, and what the components of it are. Realize which parts of your force are helping you, which are wasted, and which could possibly be hurting you!

